Grafazo: ¿Con qué alumnos puedo hacer TPs en un futuro?
Contents
Grafazo: ¿Con qué alumnos puedo hacer TPs en un futuro?#
Este grafo se encarga de analizar “camadas” de gente: grupos de alumnos que cursaron varias materias juntos.
Una vez que podamos distinguir esas camadas, ya tenemos posibles compañeros de TPs. Después, dentro de mi propia camada, con quien más quiero hacer un TP es con los alumnos que se parezcan a mí académicamente. Entonces tenemos que pasar a tener en cuenta la nota de las materias. La idea final es que yo me haga compañero de alumnos que tiendan a cursar las mismas materias que yo, y que tengamos el mismo nivel académico.
Ojo, este grafo no apunta a responder en qué materia hacer tps juntos: eso involucraría fijarse qué curso cada alumno y fijarse que personas todavía no cursaron lo mismo. La idea es un poco mas generalizada a encontrar compañeros de clase, no importa en que materia. Ya con solo ser de la misma camada sabemos que nos quedan materias en las que nos vamos a cruzar.
Por ejemplo: como Rosita y yo cursamos las mismas materias por dos años, somos de la misma camada. Y encima, como siempre nos sacamos notas parecidas, debe ser una buena compañera de TP para mí.
¿Cómo es el grafo?#
El grafo analizado va a ser un multigrafo: entre cada par de alumnos puede haber varias aristas
Nodos: alumnos
Aristas: conectar dos alumnos que hayan cursado la misma materia el mismo cuatrimestre
Peso de las aristas: la relacion entre las notas de esa cursada. Mientras más parecidos somos, más cercano estamos, y por ende menor peso hay en nuestra arista. Lo calculamos como la diferencia entre las notas.
Si me saque un 10 y vos un 10, nuestro peso es 0.
Si me saque un 4 y vos un 10, nuestro peso es 6.
En el caso de que yo estoy en final y vos aprobaste, hardcodeamos el peso a 7
import pandas as pd
df = pd.read_pickle('fiuba-map-data.pickle')
df = df.dropna(axis=1, how='all')
display(df.sample(3))
df.shape
| Padron | Carrera | Orientacion | Final de Carrera | materia_id | materia_nota | materia_cuatrimestre | optativas | aplazos | |
|---|---|---|---|---|---|---|---|---|---|
| 14476 | 102749 | informatica | Sistemas Distribuidos | tpp | 75.09 | 10.0 | NaN | NaN | NaN |
| 37739 | 102671 | informatica | Gestión Industrial de Sistemas | tpp | 75.08 | 10.0 | 2020.0 | NaN | NaN |
| 14350 | 95897 | informatica | Sistemas Distribuidos | tpp | 63.01 | 7.0 | NaN | NaN | NaN |
(21787, 9)
def corrnotas(row):
if ((row['src_nota'] == -1 and row['dst_nota'] != -1) or
(row['dst_nota'] == -1 and row['src_nota'] != -1)):
return 7
return abs(row['src_nota'] - row['dst_nota'])
df_nodes_metadata = df[["Padron", "Carrera", "aplazos", "optativas"]]
df_nodes_metadata = df_nodes_metadata[df_nodes_metadata["aplazos"].notnull() | df_nodes_metadata["optativas"].notnull()]
df_nodes_metadata = df_nodes_metadata.groupby(["Padron", "Carrera"], as_index=False).first()
df_nodes = df[["Padron", "Carrera", "Orientacion", "Final de Carrera"]]
df_nodes = df_nodes.drop_duplicates()
df_nodes = df_nodes.merge(df_nodes_metadata, how="outer")
df_nodes.set_index("Padron", inplace=True)
display(df_nodes.dropna().sample(3))
df_nodes.shape
| Carrera | Orientacion | Final de Carrera | aplazos | optativas | |
|---|---|---|---|---|---|
| Padron | |||||
| 96105 | informatica | Gestión Industrial de Sistemas | tpp | 1.0 | [{'id': 1, 'nombre': 'Aprendizaje Estadístico ... |
| 106032 | informatica | Gestión Industrial de Sistemas | tpp | 1.0 | [{'id': 1, 'nombre': 'Materia Optativa', 'cred... |
| 100566 | informatica | Sistemas Distribuidos | tpp | 1.0 | [{'id': 1, 'nombre': 'Materia Optativa', 'cred... |
(1033, 5)
from itertools import combinations
df_edges = (df[df['materia_cuatrimestre'].notnull()]
.groupby(['materia_id', 'materia_cuatrimestre'])[['Padron', 'materia_nota']]
.apply(lambda x : list(combinations(x.values,2)))
.apply(lambda x: pd.Series(x, dtype="object"))
.stack()
.reset_index(level=0, name='Usuarios')
)
df_edges = df_edges.reset_index()
df_edges[['src', 'dst']] = df_edges['Usuarios'].tolist()
df_edges[['src_padron', 'src_nota']] = df_edges['src'].tolist()
df_edges[['dst_padron', 'dst_nota']] = df_edges['dst'].tolist()
# Nos quedamos solo con las materias aprobadas (nota > 0) o en final (-1)
df_edges = df_edges[(df_edges['src_nota'] != -2) & (df_edges['src_nota'] != 0)]
df_edges = df_edges[(df_edges['dst_nota'] != -2) & (df_edges['dst_nota'] != 0)]
# Calculamos la correlacion entre las notas
df_edges['corrnotas'] = df_edges.apply(corrnotas, axis=1)
df_edges = df_edges[['src_padron', 'dst_padron', 'materia_cuatrimestre', 'materia_id', 'src_nota', 'dst_nota', 'corrnotas']]
display(df_edges.dropna().sample(3))
df_edges.shape
| src_padron | dst_padron | materia_cuatrimestre | materia_id | src_nota | dst_nota | corrnotas | |
|---|---|---|---|---|---|---|---|
| 42299 | 919191 | 100710 | 2020.5 | 71.14 | 4.0 | 4.0 | 0.0 |
| 102617 | 104415 | 101715 | 2019.0 | 75.40 | 8.0 | 6.0 | 2.0 |
| 78357 | 107024 | 103856 | 2022.5 | 75.09 | 6.0 | 4.0 | 2.0 |
(76458, 7)
import networkx as nx
import matplotlib.pyplot as plt
import utils
G = nx.from_pandas_edgelist(df_edges,
source='src_padron',
target='dst_padron',
edge_attr=['materia_id','materia_cuatrimestre', 'corrnotas'],
create_using=nx.MultiGraph())
nx.set_node_attributes(G, df_nodes.to_dict('index'))
utils.stats(G)
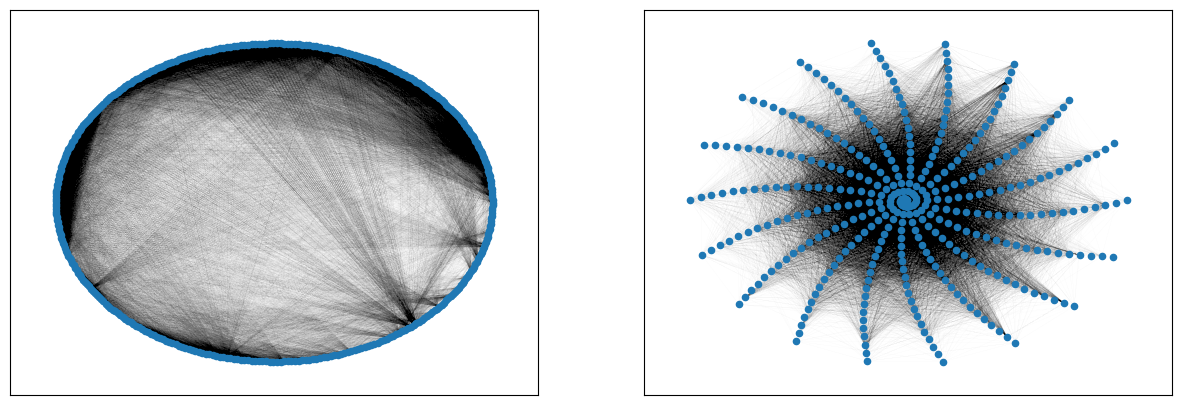
utils.plot(G)
MultiGraph with 379 nodes and 76458 edges
El diámetro de la red: 5
El grado promedio de la red: 403.47
Puentes globales: [('100866', '99796'), ('98600', '109670')]
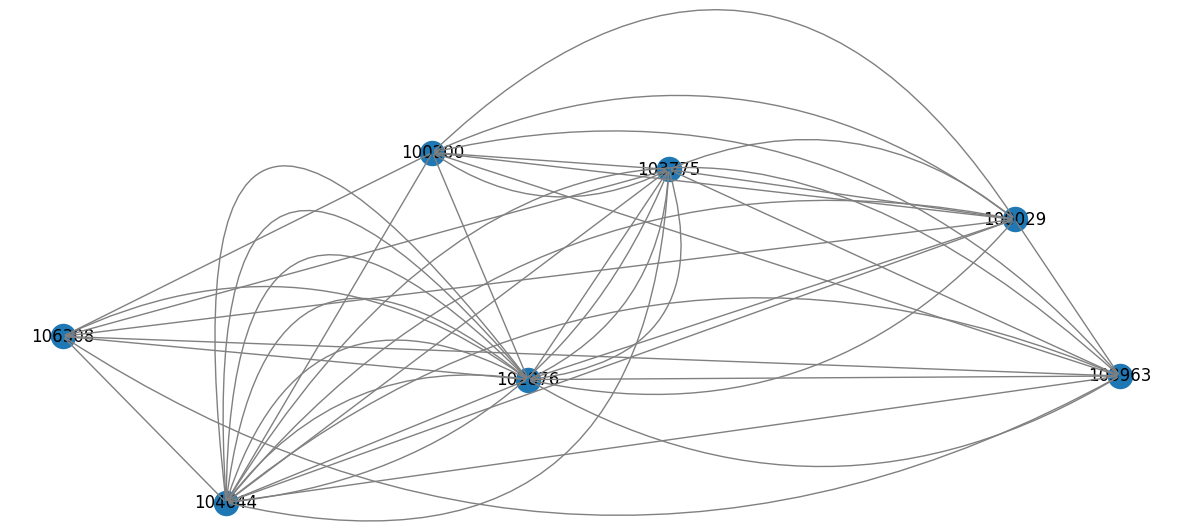
from config import PADRON
# Aprovechando que este es un multigrafo, mostremos las multiples aristas que hay en una cantidad pequeña de alumnos
cliques = nx.find_cliques(G, [PADRON])
min_clique = nx.subgraph(G, min(cliques, key=len))
# Robadisimo de: https://stackoverflow.com/a/60638452
pos = nx.random_layout(min_clique)
nx.draw_networkx_nodes(min_clique, pos)
nx.draw_networkx_labels(min_clique, pos)
ax = plt.gca()
for e in min_clique.edges:
ax.annotate("",
xy=pos[e[0]], xycoords='data',
xytext=pos[e[1]], textcoords='data',
arrowprops=dict(arrowstyle="-", color="0.5",
connectionstyle="arc3,rad=rr".replace('rr',str(0.3*e[2]))))
plt.axis('off')
plt.show()
Homofilia#
La homofilia nos explica una forma en la que los vínculos se forman. Esto puede depender de diferentes características, por ejemplo podemos unir personas por género, edad, nacionalidad, intereses, creencias
Lo primero que debemos hacer antes de agrupar nodos de nuestro grafo creado es un análisis teórico: ¿cómo deberían quedar segmentados los nodos y vínculos?
Las comunidades que se van a formar en nuestro grafo deberían seguir un criterio orgánico: los distintos grupos de nodos van a compartir características entre sí. Cuando pensamos en personas en la vida cotidiana y cómo estas podrían vincularse, lo más natural es pensar en edad, ideología, etc. Cuando pensamos en alumnos de una universidad a lo largo de su carrera, no siempre es eso lo que une a la gente.
En este caso, los grupos que se van a formar son los de las camadas. Estas camadas, teóricamente, deberían tender a ser alumnos con padrones cercanos. Esto es porque el padrón es un número incremental, entonces si vos y yo tenemos un +-1 de diferencia en el padrón, nos anotamos el mismo dia a la facultad. Y si nos anotamos el mismo dia a la facultad, probablemente vayamos juntos a la par en la carrera y nos crucemos seguido en materias.
Es decir, más menos algunas anomalías, deberíamos ver una relación entre el número de padrón y los grupos formados.
Como las comunidades se van a formar en base a las aristas que hay entre los nodos, tenemos que confirmar que la proporción de aristas tiene sentido. Es decir, la frecuencia de aristas entre nodos de distintas camadas teóricas deberia acercarse a la frecuencia de aristas entre nodos de lo que hay en el grafo.
Antes de agrupar los nodos, corramos un análisis sobre el alumnado y veamos como se dividen según su número de padrón. Para este análisis vamos a dividir al alumnado en 4 camadas. La camada número 1 estará compuesta por aquellos padrones que comienzan con 100 o inferiores. Las siguientes camadas son desde los padrones 101 a 104; de 105 a 109; y de 110 a 120.
df_camadas = df_edges.copy()
def definir_camada(f):
if not f.isnumeric():
return 0
f = int(f)
if f in range(900,999) or f == 100:
return 1
if f in range(101, 105):
return 2
if f in range(105, 110):
return 3
if f in range(110, 120):
return 4
return 0
df_camadas['src_camada'] = df_camadas.apply(lambda f: definir_camada(str(f.src_padron)[:3]), axis=1)
df_camadas['dst_camada'] = df_camadas.apply(lambda f: definir_camada(str(f.dst_padron)[:3]), axis=1)
df_camadas = df_camadas[df_camadas['src_camada'] > 0]
df_camadas = df_camadas[df_camadas['dst_camada'] > 0]
df_camadas = df_camadas[['src_padron', 'dst_padron', 'src_camada', 'dst_camada']]
df_camadas.sample(4)
| src_padron | dst_padron | src_camada | dst_camada | |
|---|---|---|---|---|
| 112688 | 106223 | 106004 | 3 | 3 |
| 107992 | 109404 | 109667 | 3 | 3 |
| 88556 | 105931 | 107044 | 3 | 3 |
| 12933 | 108485 | 106005 | 3 | 3 |
Valores teóricos esperados#
Se deberá realizar al siguente ecuación para encontrar las probabilidades de camadas entre cada dos nodos
Luego, la probabilidad de ser de la camada 1 y compartir con alguien de la camada 1 es \(\mathbb{P}(Camada1)^2\), mientras que cruzarse entre camadas te da una probabilidad de \(\mathbb{P}(Camada1) \cdot \mathbb{P}(Camada2) \cdot 2\)
(
df_camadas.pivot_table(
index='src_camada',
columns='dst_camada',
values='src_padron',
aggfunc='count'
) / len(df_camadas)
)
| dst_camada | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| src_camada | ||||
| 1 | 0.117740 | 0.092984 | 0.022244 | 0.000290 |
| 2 | 0.122256 | 0.239981 | 0.064148 | 0.002483 |
| 3 | 0.025903 | 0.111061 | 0.191355 | 0.000581 |
| 4 | 0.002076 | 0.006040 | 0.000726 | 0.000131 |
Valores encontrados#
df_temp = df_camadas.drop_duplicates(subset='src_padron')
total_nodos = df_temp.shape[0]
df_prob = df_temp.groupby(['src_camada']).count()[["src_padron"]].apply(lambda x: (x/total_nodos) ** 2).rename(columns={'src_padron':'P(misma camada)'})
df_prob
| P(misma camada) | |
|---|---|
| src_camada | |
| 1 | 0.037281 |
| 2 | 0.129766 |
| 3 | 0.186863 |
| 4 | 0.000208 |
Se calcula el threshold teórico considerando 4 camadas para una arista entre dos alumnos de distintas camadas
probabilidad_intercamada = (1 - df_prob.sum()).squeeze()
print(f'''Threshold teórico: {round(probabilidad_intercamada, 2)}''')
Threshold teórico: 0.65
df_prob_aristas = df_camadas[df_camadas['src_camada'] != df_camadas['dst_camada']]
aristas_intercamadas = df_prob_aristas.shape[0]
aristas_totales = df_camadas.shape[0]
probabilidad_intercamada_experimental = aristas_intercamadas / aristas_totales
print(f'''Proporción existente de "sin homofilia": {round(probabilidad_intercamada_experimental/probabilidad_intercamada * 100, 2)}%''')
Proporción existente de "sin homofilia": 69.79%
Esta proporción resulta alta en relación a lo que obtuvimos teóricamente, y creemos que se debe a que planteamos camadas muy grandes, que en la práctica deberían subdividirse en más camadas, y por lo tanto, resulta más difícil que haya tanta conexión entre camadas.
Comunidades#
Ahora que ya sabemos que los vínculos entre los nodos efectivamente son una representación real de lo que nosotros llamamos camadas, solo nos queda dividir el grafo en comunidades, confirmar que cada comunidad se refiere a una camada, e indagar sobre cada comunidad por separado, ya pudiendo tratar a cada una como una camada distinta.
from networkx.algorithms import community
# La primera corrida solo calculamos camadas, sin darle peso a las notas. Pasamos `weight=None` a louvain
louvain = community.louvain_communities(G, weight=None)
utils.plot_communities(G, louvain)
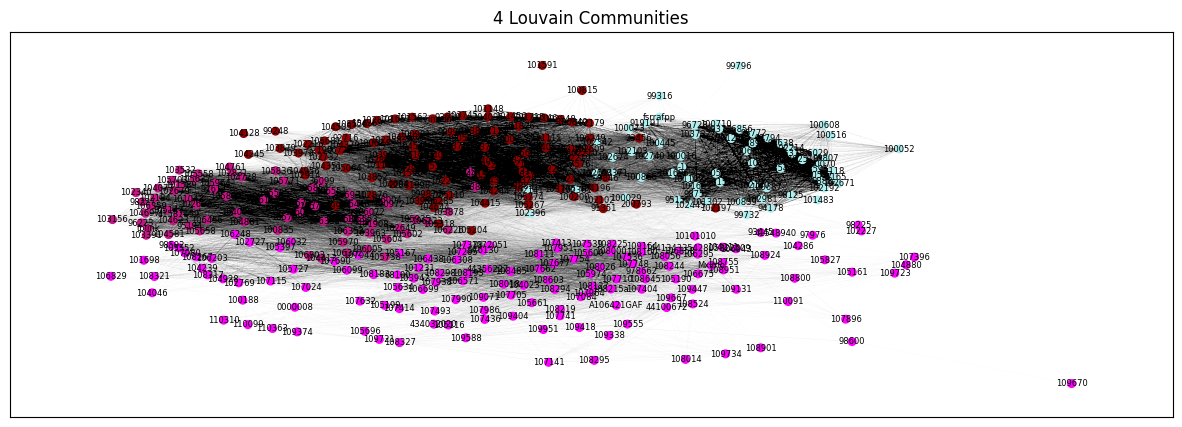
Evaluación de comunidades#
¿Efectivamente se refieren a distintas camadas de alumnos? ¿Alumnos que ingresaron a la facultad al mismo tiempo?
¿Existe correlación entre la distribución de padrones y la comunidad?
import seaborn as sns
import numpy as np
louvain_padrones = []
for i, comunidad in enumerate(louvain):
for padron in comunidad:
louvain_padrones.append((padron, i))
df_comunidades = pd.DataFrame(louvain_padrones, columns=["padron", "comunidad"])
# len patch for overflow
df_temp = df_comunidades[(df_comunidades['padron'].str.isdigit()) & (df_comunidades["padron"].str.len() >= 5) & (df_comunidades["padron"].str.len() <= 6)].copy()
df_temp["padron"] = df_temp["padron"].astype(int)
# sacar outliers por percentiles, robado de from https://stackoverflow.com/a/59366409
Q1 = df_temp["padron"].quantile(0.10)
Q3 = df_temp["padron"].quantile(0.90)
IQR = Q3 - Q1
df_comunidades = df_temp[~((df_temp["padron"] < (Q1 - 1.5 * IQR)) |(df_temp["padron"] > (Q3 + 1.5 * IQR)))]
display(df_comunidades.sample(3))
display(df_comunidades.groupby('comunidad').agg({'padron':[np.mean,np.std,'count']}))
g = sns.displot(
df_comunidades,
x="padron",
col="comunidad",
element="step",
stat="count",
common_norm=False,
)
| padron | comunidad | |
|---|---|---|
| 255 | 109723 | 3 |
| 27 | 99796 | 0 |
| 144 | 91351 | 1 |
| padron | |||
|---|---|---|---|
| mean | std | count | |
| comunidad | |||
| 0 | 99896.229508 | 2816.161935 | 61 |
| 1 | 102371.739583 | 3124.528482 | 96 |
| 2 | 104326.104478 | 2485.639599 | 67 |
| 3 | 106842.222222 | 2760.319604 | 126 |
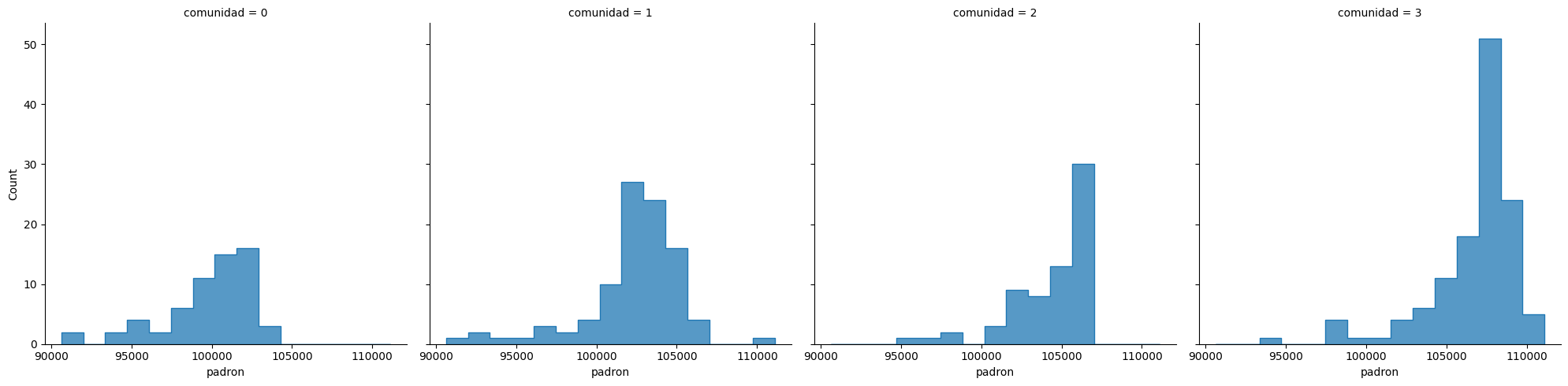
Se puede observar una mínima correlación considerando el intervalo más frecuente de cada comunidad. Esto coincide con lo que se planteo con el concepto de homofilia.
Alumnos similares dentro de la misma camada#
Ahora que ya tenemos cada comunidad de gente que cursó junta, queremos encontrar dentro de estos subgrafos los alumnos que tengan notas similares. O sea, ya sé que soy parte de una camada de 100 personas. De esas 100, ¿con quién me conviene hacer un TP?
Entonces vamos a volver a calcular comunidades, pero esta vez lo hacemos dentro de cada camada y teniendo en cuenta el peso de las aristas, que representan la similitud académica.
def nestedsearch(el, lst_of_sets):
return list(filter(lambda lst: el in lst, lst_of_sets))[0]
def armar_grupo(padron):
camada = nestedsearch(padron, louvain)
subnetwork = nx.subgraph(G, camada)
min_alumnos, max_alumnos = 6, 14
max_iteraciones = 25
i = 0
grupo = []
for i in range(max_iteraciones):
sublouvains = community.louvain_communities(subnetwork, weight='corrnotas', resolution=1+(i*0.01))
comunidad = nestedsearch(padron, sublouvains)
if min_alumnos <= len(comunidad) <= max_alumnos:
grupo = comunidad
break
elif not grupo or (len(comunidad) >= max_alumnos and (len(comunidad) - max_alumnos <= len(grupo) - max_alumnos)):
grupo = comunidad
i+=1
return grupo
grupo = armar_grupo(PADRON)
subgraph = nx.subgraph(G, grupo)
colors = []
for n in subgraph.nodes:
if n == PADRON: colors.append('#c0a9e2')
else: colors.append('#1f78b4')
plt.figure(figsize=(12,6))
plt.title(f"Posibles compañeros de TP de {PADRON}")
nx.draw_networkx(
subgraph,
width=0.02,
node_color=colors,
font_size=16,
)
plt.show()
grupo.remove(PADRON)
print(f"Posibles compañeros de {PADRON}: {grupo}")
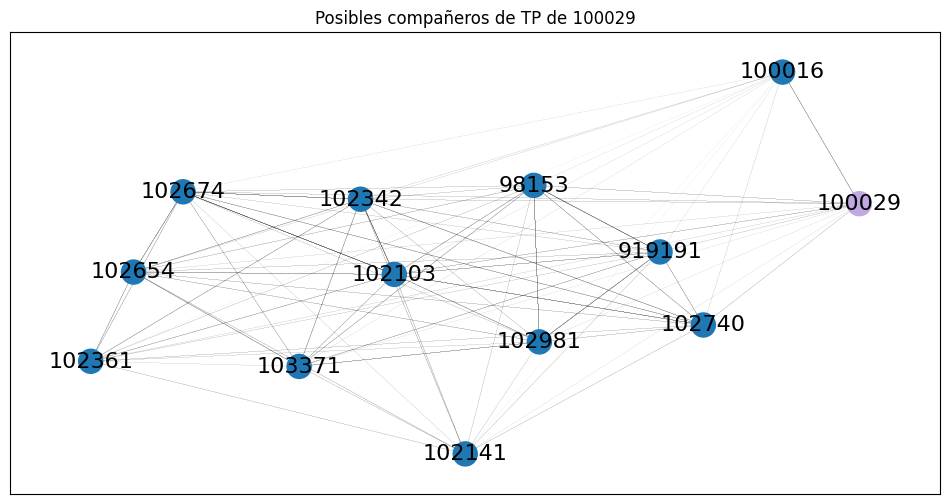
Posibles compañeros de 100029: {'102981', '102674', '102740', '102342', '102141', '102361', '102103', '103371', '102654', '98153', '100016', '919191'}
