Graphito: ¿Qué características tiene el FIUBA-Map como red social?
Contents
Graphito: ¿Qué características tiene el FIUBA-Map como red social?#
A lo largo del trabajo práctico vamos a generar diferentes grafos con el set de datos de alumnos de FIUBA. Pero para poder hacer estos análisis, queremos asegurarnos que los datos que tenemos se asemejen a los de una red social, para así poder utilizar los recursos que conocemos para análisis de redes sociales. Así que, para dar un primer pantallazo, vamos a conectar a aquellos alumnos que cursaron juntos alguna materia en un mismo cuatrimestre, de manera tal que los alumnos (nodos) se conectan si alguna vez cursaron juntos una materia (aristas), y a partir de ello vamos a hacer un análisis general de la misma:
¿Cuál es su diámetro (largo máximo de todos los caminos mínimos)?
¿Cuál es el grado promedio? ¿Les alumnes tienden a tener muchas conexiones, es decir que tienden a hacer las mismas materias con las mismas personas? ¿Cómo se distribuyen los grados?
¿Cuál es el coeficiente de clustering? ¿Mis amigues son amigues entre sí?
¿Tiene una componente gigante?
¿Es una red aleatoria?
¿Cómo evoluciona nuestra red, considerando el factor temporal de los cuatrimestres?
¿Cómo es el grafo?#
El grafo va a ser simple sin pesos
Nodos: Alumnos
Aristas: Conectar dos alumnos que hayan cursado la misma materia el mismo cuatrimestre
Set up#
import pandas as pd
import utils
df = pd.read_pickle('fiuba-map-data.pickle')
df = df.dropna(axis=1, how='all')
display(df.sample(3))
df.shape
| Padron | Carrera | Orientacion | Final de Carrera | materia_id | materia_nota | materia_cuatrimestre | optativas | aplazos | |
|---|---|---|---|---|---|---|---|---|---|
| 32063 | 106223 | informatica | NaN | tesis | 75.09 | 8.0 | 2021.5 | NaN | NaN |
| 90700 | cmtbx212 | informatica | NaN | NaN | 75.07 | -1.0 | NaN | NaN | NaN |
| 62370 | 751287611aplfjroqmvn | informatica | Gestión Industrial de Sistemas | tpp | 61.10 | -1.0 | NaN | NaN | NaN |
(21787, 9)
df_nodos = df[["Padron", "materia_id", "materia_cuatrimestre"]]
# Sacamos a aquellos que no ordenan su carrera por cuatrimestres
df_nodos.dropna(subset=['materia_cuatrimestre'], inplace=True)
# Sacamos a aquellos que solo agregaron 1 o 2 cuatrimestres en materias a modo de prueba
df_nodos = df_nodos.groupby(['Padron']).filter(lambda x: len(x)>2)
display(df_nodos.sample(3))
df_nodos.shape
| Padron | materia_id | materia_cuatrimestre | |
|---|---|---|---|
| 90373 | 106438 | 61.08 | 2021.0 |
| 40538 | 102361 | 66.69 | 2023.0 |
| 24828 | 107964 | 75.16 | 2026.0 |
(9759, 3)
df_red = utils.construir_df_pareando_padrones_por(df_nodos, 'materia_cuatrimestre')
df_red = df_red.sort_values('materia_cuatrimestre')
df_red = df_red.drop_duplicates(['Padron_min', 'Padron_max'], keep='first').reset_index()
df_red = df_red[['Padron_x', 'Padron_y', 'materia_id', 'materia_cuatrimestre']]
df_red.rename(columns = {'Padron_x':'src_padron', 'Padron_y':'dst_padron'}, inplace = True)
display(df_red.sample(3))
df_red.shape
| src_padron | dst_padron | materia_id | materia_cuatrimestre | |
|---|---|---|---|---|
| 17669 | 107951 | 102876 | 61.09 | 2022.0 |
| 14932 | 104393 | 105742 | 75.09 | 2021.5 |
| 16192 | 108100 | 108603 | 75.41 | 2021.5 |
(31256, 4)
import networkx as nx
import matplotlib.pyplot as plt
G = nx.from_pandas_edgelist(df_red,
source='src_padron',
target='dst_padron',
create_using=nx.Graph())
nx.set_node_attributes(G, df_red.to_dict('index'))
print(G)
Graph with 393 nodes and 31256 edges
Datos del Grafo#
Diámetro#
from utils import md
md(f"""El **diámetro** de nuestra red es de {nx.diameter(G)}, y tiene mucho sentido que sea un número tan chico porque el FIUBA Map tiene cargadas las notas de alumnos desde el 2014 en adelante (aproximadamente), así que no hay tantas camadas de alumnos, sumado a que estamos filtrando por una carrera. Además de esto, los alumnos avanzan en la carrera a diferentes velocidades, por lo que hay recursantes que cursan con varias camadas. Teniendo en cuenta estos tres factores, hace que la mayoría de los nodos en el grafo están muy conectados. Es interesante también ver que la **distancia promedio de la red** de nuestra red es de {nx.average_shortest_path_length(G)}, lo cual se relaciona mucho a tener un diámetro tan pequeño.\n""")
utils.plot_diametro(G)
El diámetro de nuestra red es de 3, y tiene mucho sentido que sea un número tan chico porque el FIUBA Map tiene cargadas las notas de alumnos desde el 2014 en adelante (aproximadamente), así que no hay tantas camadas de alumnos, sumado a que estamos filtrando por una carrera. Además de esto, los alumnos avanzan en la carrera a diferentes velocidades, por lo que hay recursantes que cursan con varias camadas. Teniendo en cuenta estos tres factores, hace que la mayoría de los nodos en el grafo están muy conectados. Es interesante también ver que la distancia promedio de la red de nuestra red es de 1.6001843485485798, lo cual se relaciona mucho a tener un diámetro tan pequeño.

Grado (Promedio y Distribución)#
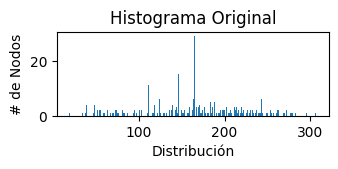
md(f"""El **grado promedio de la red** es de {sum([n[1] for n in G.degree()]) / len(G):.2f}. Sin embargo la distribución de los grados es uniforme, y eso se debe a que por un lado tenemos alumnes con gran antigüedad (los que escriben este TP) y por otro lado alumnes que recién arrancan las cursadas. Es interesante pensar, que a medida que los años pasen, la distribución va a inclinarse más a los números altos (que es algo que ya podemos notar).\n""")
utils.plot_distribucion_grados([G])
El grado promedio de la red es de 159.06. Sin embargo la distribución de los grados es uniforme, y eso se debe a que por un lado tenemos alumnes con gran antigüedad (los que escriben este TP) y por otro lado alumnes que recién arrancan las cursadas. Es interesante pensar, que a medida que los años pasen, la distribución va a inclinarse más a los números altos (que es algo que ya podemos notar).
Clustering#
md(f"""El **clustering** es la probabilidad de que dos vértices adyacentes de A sean adyacentes entre sí. El clustering promedio de esta red es {"%3.4f"%nx.average_clustering(G)}. En redes sociales tenemos en general un coeficiente de Clustering alto, aca podemos notar uno bastante alto. Un ejemplo claro es nuestra bella amistad con uno de los integrantes del trabajo. Un amigue A curso con B y nos presentó a B, desde entonces cursamos todas las materias juntes. """)
utils.plot_clustering(G)
El clustering es la probabilidad de que dos vértices adyacentes de A sean adyacentes entre sí. El clustering promedio de esta red es 0.6995. En redes sociales tenemos en general un coeficiente de Clustering alto, aca podemos notar uno bastante alto. Un ejemplo claro es nuestra bella amistad con uno de los integrantes del trabajo. Un amigue A curso con B y nos presentó a B, desde entonces cursamos todas las materias juntes.

Componente conexa#
md(f"""Por último, la componente {"es conexa" if nx.is_connected(G) else "no es conexa"}, es decir que tenemos una **componente gigante**.\n""")
Por último, la componente es conexa, es decir que tenemos una componente gigante.
Simulación de modelados#
Ahora, vamos a realizar una simulación de un modelado de Erdös-Rényi y un modelado de Preferential Attachment (ley de potencias) que correspondan a los parámetros de nuestra red, para luego poder compararlos y poder entender si nuestra red es aleatoria. Para eso vamos a conocer el diámetro, grado promedio, distancia promedio, clustering promedio y si se trata de una componente gigante. Al finalizar, vamos realizar una representación de anonymous walks para cada una de las redes y vamos a determinar por distancia coseno cuál sería la simulación más afín y por qué.
El modelo Erdös-Rényi se utiliza para crear redes aleatorias en las redes sociales. En el modelo Erdös-Rényi, se tiene que un nuevo nodo se enlaza con igual probabilidad con el resto de la red, es decir posee una independencia estadística con el resto de nodos de la red
Para el modelo de Preferential Attachment usamos un algoritmo que se denomina Modelo de Barabási–Albert el cual genera redes aleatorias complejas empleando una regla o mecanismo denominado conexión preferencial. Las redes generadas por este algoritmo poseen una distribución de grado de tipo potencia.
Erdös Renyi#
g_erdos = nx.erdos_renyi_graph(G.number_of_nodes(), 0.6)
print(f"""
Red aleatoria Erdös-Renyi
El diámetro de la red: {nx.diameter(g_erdos)}
El grado promedio de la red: {sum([n[1] for n in g_erdos.degree()]) / len(g_erdos):.2f}
La distancia promedio de la red: {nx.average_shortest_path_length(g_erdos)}
Clustering promedio: {"%3.4f"%nx.average_clustering(g_erdos)}
Puentes globales: {list(nx.bridges(g_erdos))}
{"Es conexa" if nx.is_connected(g_erdos) else "No es conexa"}
""")
Red aleatoria Erdös-Renyi
El diámetro de la red: 2
El grado promedio de la red: 234.92
La distancia promedio de la red: 1.4007244119021653
Clustering promedio: 0.5995
Puentes globales: []
Es conexa
Preferential Attachment#
g_preferential_attachment = nx.barabasi_albert_graph(G.number_of_nodes(), G.number_of_nodes()//G.number_of_nodes())
print(f"""
Red aleatoria Preferential Attachment
El diámetro de la red: {nx.diameter(g_preferential_attachment)}
El grado promedio de la red: {sum([n[1] for n in g_preferential_attachment.degree()]) / len(g_preferential_attachment):.2f}
La distancia promedio de la red: {nx.average_shortest_path_length(g_preferential_attachment)}
Clustering promedio: {nx.average_clustering(g_preferential_attachment)}
{"Es conexa" if nx.is_connected(g_preferential_attachment) else "No es conexa"}
""")
Red aleatoria Preferential Attachment
El diámetro de la red: 15
El grado promedio de la red: 1.99
La distancia promedio de la red: 6.461520486057018
Clustering promedio: 0.0
Es conexa
Anonymous Walks#
aw_erdos = utils.anonymous_walks(g_erdos)
aw_preferential = utils.anonymous_walks(g_preferential_attachment)
aw_original = utils.anonymous_walks(G)
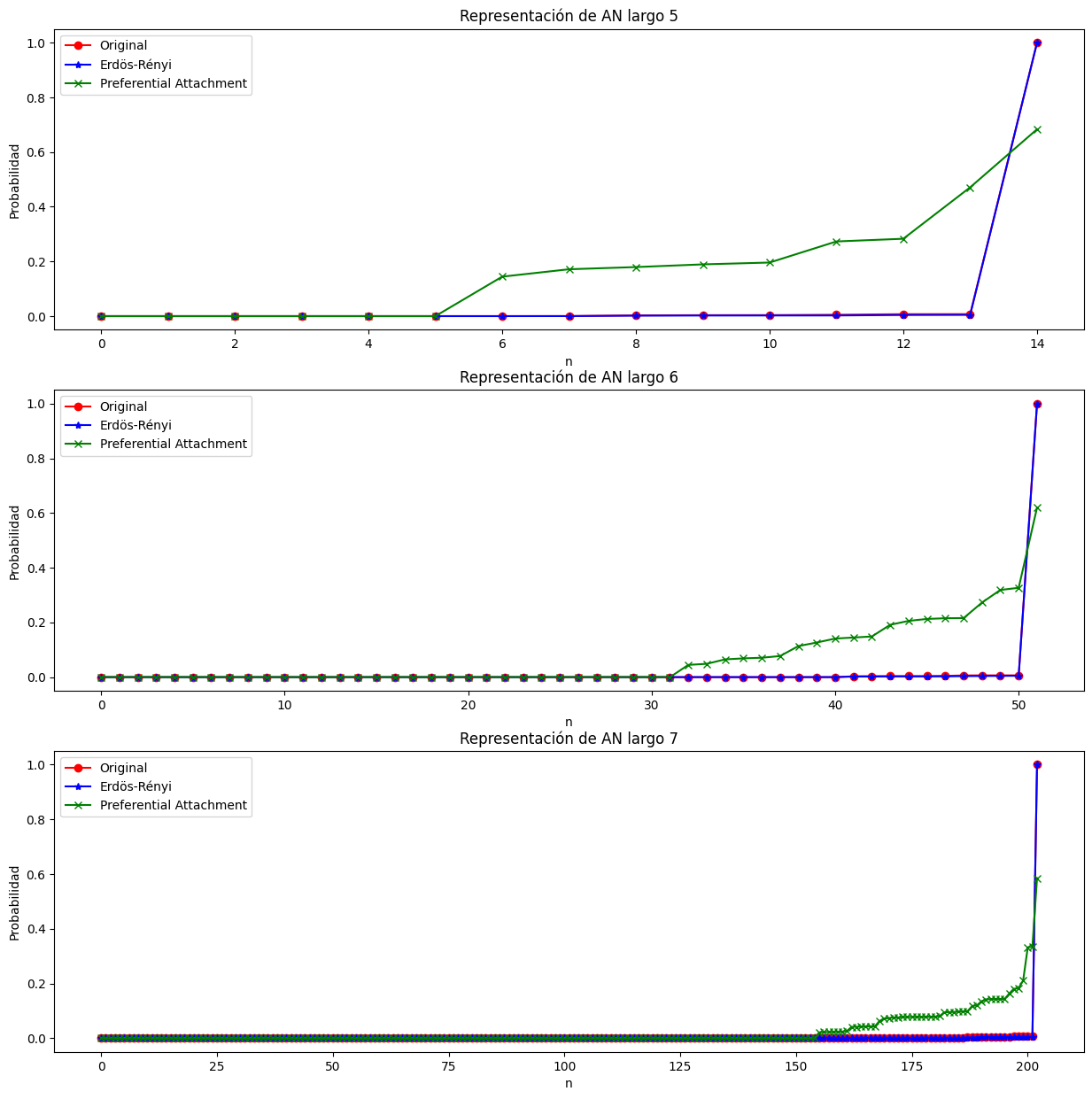
utils.plot_anonymous_walks([aw_original, aw_erdos, aw_preferential])
from numpy import linalg as LA
import numpy as np
md(f"""
Las leyes de potencias aparecen de la **ventaja acumulativa**. Esto puede verse como un desbalance desproporcionado entre los que tienen muchos contactos, y los que tienen pocos. Es claro que el grafon no iba a ser similar a el grafo generado por Barabási–Albert, ya que no tiene sentido que un alumno tenga muchísimas aristas, mientras que otros tengan pocas ya que hay muchas materias en común. La distancia de coseno entre nuestro grafon y el grafo aleatorio es de {1 - np.inner(aw_original[7], aw_preferential[7]) / (LA.norm(aw_original[7]) * LA.norm( aw_preferential[7]))}. \n
En cambio, al compararlo con el grafo generado con Erdös Renyi, podemos encontrar más similitudes. A diferencia del anterior, todos los nodos tienen probabilidad de contar con muchas aristas, dejando un grafo más real y parecido a una red de una Universidad en donde todos los alumnos tienden a cursar materias similares. La distancia de coseno entre los mismos {1 - np.inner(aw_original[7], aw_erdos[7]) / (LA.norm(aw_original[7]) * LA.norm(aw_erdos[7]))}
""")
Las leyes de potencias aparecen de la ventaja acumulativa. Esto puede verse como un desbalance desproporcionado entre los que tienen muchos contactos, y los que tienen pocos. Es claro que el grafon no iba a ser similar a el grafo generado por Barabási–Albert, ya que no tiene sentido que un alumno tenga muchísimas aristas, mientras que otros tengan pocas ya que hay muchas materias en común. La distancia de coseno entre nuestro grafon y el grafo aleatorio es de 0.9752541893257213.
En cambio, al compararlo con el grafo generado con Erdös Renyi, podemos encontrar más similitudes. A diferencia del anterior, todos los nodos tienen probabilidad de contar con muchas aristas, dejando un grafo más real y parecido a una red de una Universidad en donde todos los alumnos tienden a cursar materias similares. La distancia de coseno entre los mismos 1.650459504176638e-05
utils.plot_distribucion_grados([G, g_erdos, g_preferential_attachment])

Evolución del FIUBA-Map#
Los resultados obtenidos hasta ahora parten de “una foto” de una red social armada a partir del FIUBA map. Eso alcanza para hacer análisis muy interesantes, sacar conclusiones y hasta contestar muchas preguntas.
Pero en nuestro set de datos contamos con un factor temporal inherente al dominio del problema con el que estamos tratando: los cuatrimestes. Es por eso que decidimos aprovechar esta particularidad y hacer un análisis para ver cómo evoluciona la red del FIUBA map cuatrimestre a cuatrimeste.
Para ello vamos a estudiar la evolución del grafo con el que estamos trabajando.
from datetime import datetime
# tomamos los cuatrimestres hasta la actualidad, sin tener en cuenta cuatrimestres que no pasaron porque la cantidad de nodos se mantiene constante
curr_year = datetime.now().year
curr_month = datetime.now().month
curr_cuatri = curr_year if curr_month < 3 else curr_year + 0.5
df_red = df_red.sort_values(by=['materia_cuatrimestre'])
cuatris = df_red[df_red['materia_cuatrimestre'] < curr_cuatri]['materia_cuatrimestre'].unique()
cuatris
array([2016. , 2016.5, 2017. , 2017.5, 2018. , 2018.5, 2019. , 2019.5,
2020. , 2020.5, 2021. , 2021.5, 2022. , 2022.5])
graphs = []
stats = []
# Generamos grafos y estadísticas para los últimos 12 cuatrimestres
for cuatri in cuatris[-12:]:
df_cuatri = df_red[df_red['materia_cuatrimestre'] <= cuatri]
G = nx.from_pandas_edgelist(df_cuatri,
source='src_padron',
target='dst_padron',
create_using=nx.Graph())
graphs.append((cuatri, G))
diameter = nx.diameter(G) if nx.is_connected(G) else "No conexo"
stats.append([cuatri, len(G), len(G.edges), diameter, f"{sum([n[1] for n in G.degree()]) / len(G):.2f}"])
stats = pd.DataFrame(stats, columns=['Cuatrimestre','Nodos','Aristas', 'Diametro', 'Grado promedio'])
print(stats.to_string(index=False), end='\n\n')
n = 6
fig, axs = plt.subplots(ncols=n, nrows=len(graphs)//n, figsize=(30,10))
ax = axs.flatten()
for i, g in enumerate(graphs):
ax[i].set_title(g[0])
nx.draw_networkx(g[1], pos=nx.kamada_kawai_layout(G), width=0.1 if i < 5 else 0.01, node_size=20, with_labels=False, ax=ax[i])
Cuatrimestre Nodos Aristas Diametro Grado promedio
2017.0 16 57 4 7.12
2017.5 19 71 4 7.47
2018.0 38 273 4 14.37
2018.5 82 1703 3 41.54
2019.0 141 4001 3 56.75
2019.5 166 5174 3 62.34
2020.0 233 8755 3 75.15
2020.5 265 10600 4 80.00
2021.0 311 13545 4 87.11
2021.5 328 16643 4 101.48
2022.0 350 20519 3 117.25
2022.5 386 25962 3 134.52
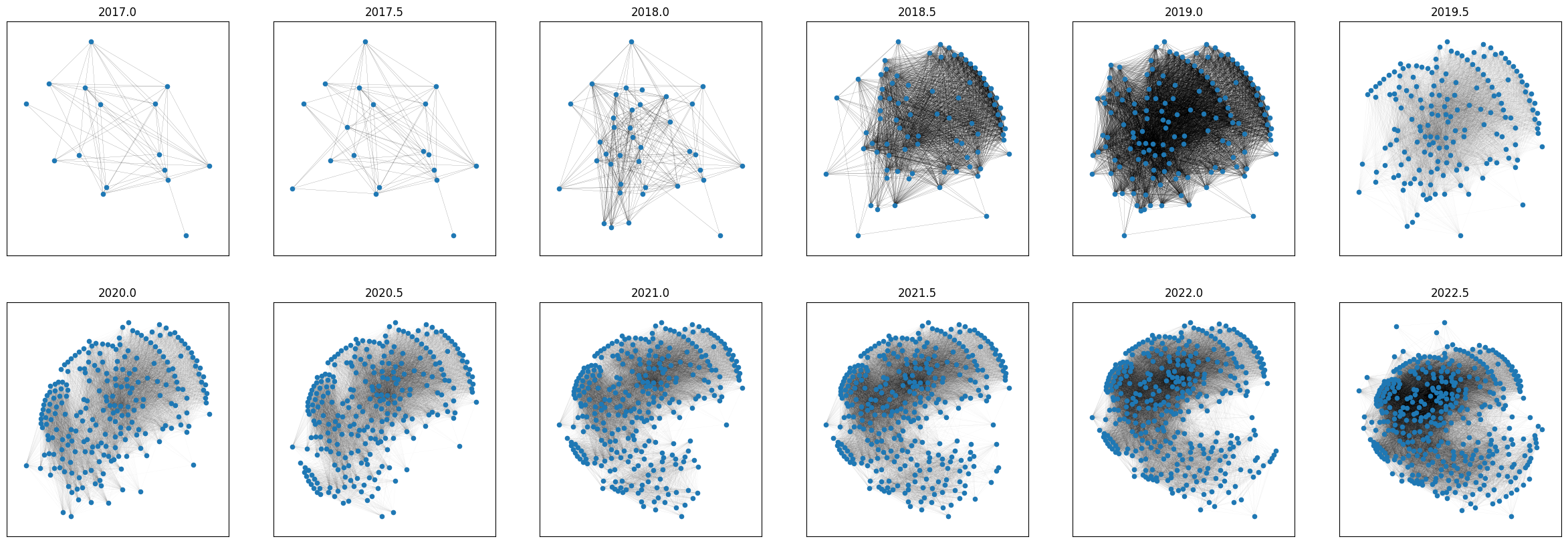
Lo primero que podemos notar es que, a lo largo del tiempo, las aristas crecen mucho más rápido que los nodos (ya veremos en qué proporción), y a su vez, el diámetro se mantiene constante casi durante toda la evolución del grafo. De la mano con esto, el grado promedio de la red va en aumento, a cada paso de la evolución.
Evolución macroscópica#
Para entender más en profundidad esta evolución, analizaremos algunos de los indicadores principales como la cantidad de nodos y aristas, el diámetro y los grados de los nodos a lo largo del tiempo.
A continuación analizaremos la relación entre la cantidad de nodos y la cantidad de aristas a lo largo del tiempo
utils.plot_evolucion_macroscopica(graphs)
Alpha es 1.94
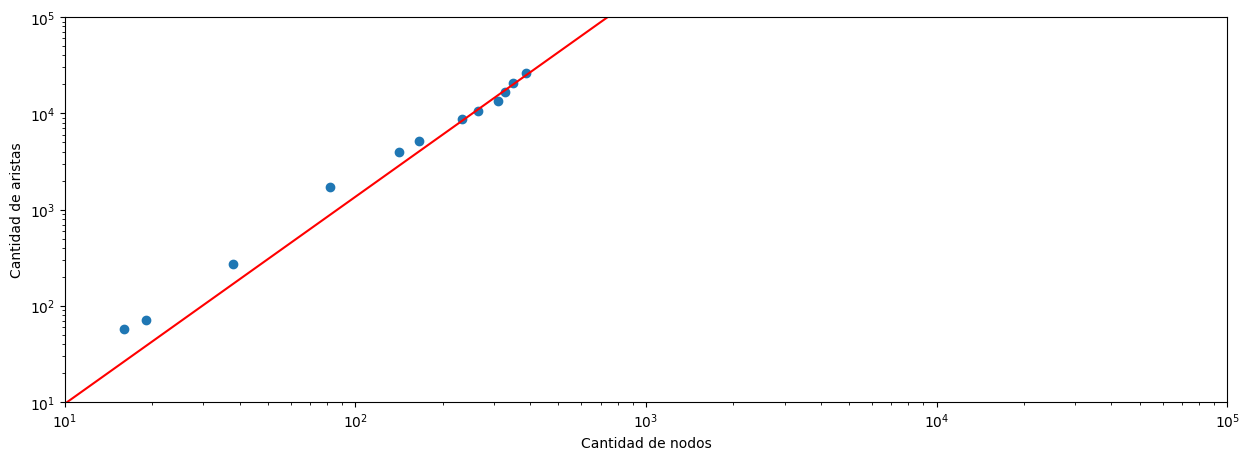
Sabemos que para la mayoría de las redes reales, la evolución de las aristas con respecto a la evolución de los nodos sigue la ley de potencia de densificación:
Donde \(\alpha\) es el exponente de densificación en el rango de [1, 2]. En nuestro caso, \(\alpha\) es mucho mayor a 1, lo que significa que a medida que evoluciona la red, el grado promedio de los nodos va vertiginosamente en aumento. Esto se condice con los grados promedios que salen de la tabla de evolución obtenida más arriba.
Para obtener más información, analicemos el diámetro.
# Eliminamos los grafos no conexos (si los hay)
diam_graphs = list(graphs)
for i in range(len(graphs))[::-1]:
if stats.iloc[i]['Diametro'] == 'No conexo':
diam_graphs.pop(i)
x = [g[0] for g in diam_graphs]
y = [nx.diameter(g[1]) for g in diam_graphs]
plt.xlabel("Cuatrimestre")
plt.ylabel("Diámetro")
plt.plot(x, y, '-o')
plt.show()
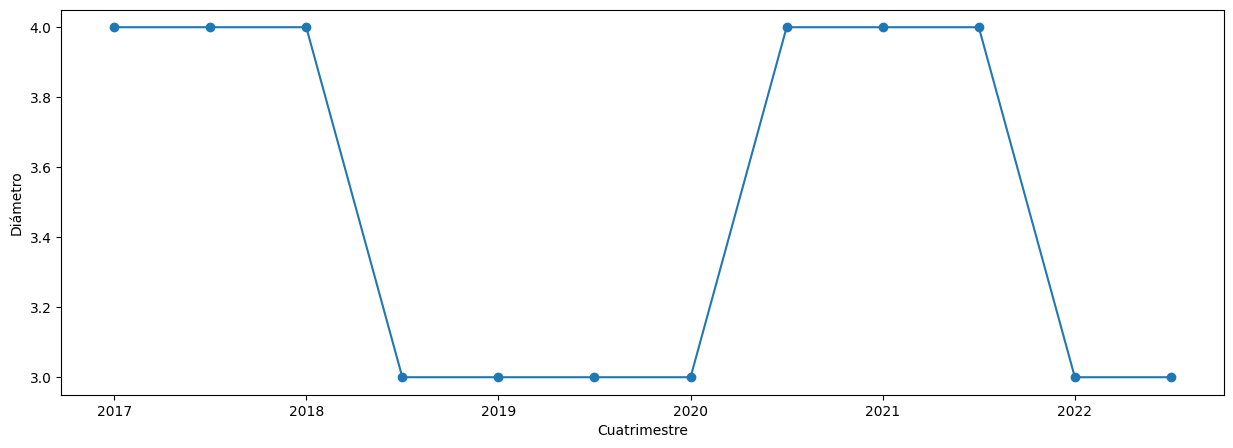
Se observa que el diámetro oscila entre 3 y 4 hasta el final para los cuatrimestres evaluados.
Si tuviéramos un grafo de Erdös-Rényi, el diámetro crecería a pesar de una alta densificación, por lo cual, para esclarecer este asunto, estudiaremos también la distribución de los grados de los nodos.
degrees = [(g[0], sorted((d for n, d in g[1].degree()), reverse=True)) for g in graphs]
fig, axs = plt.subplots(ncols=n, nrows=len(graphs)//n, figsize=(30,10))
ax = axs.flatten()
for i, degree in enumerate(degrees):
ax[i].set_xlabel("Grado del nodo")
ax[i].set_ylabel("Cantidad de nodos")
ax[i].set_title(degree[0])
ax[i].bar(*np.unique(degree[1], return_counts=True)[::-1])
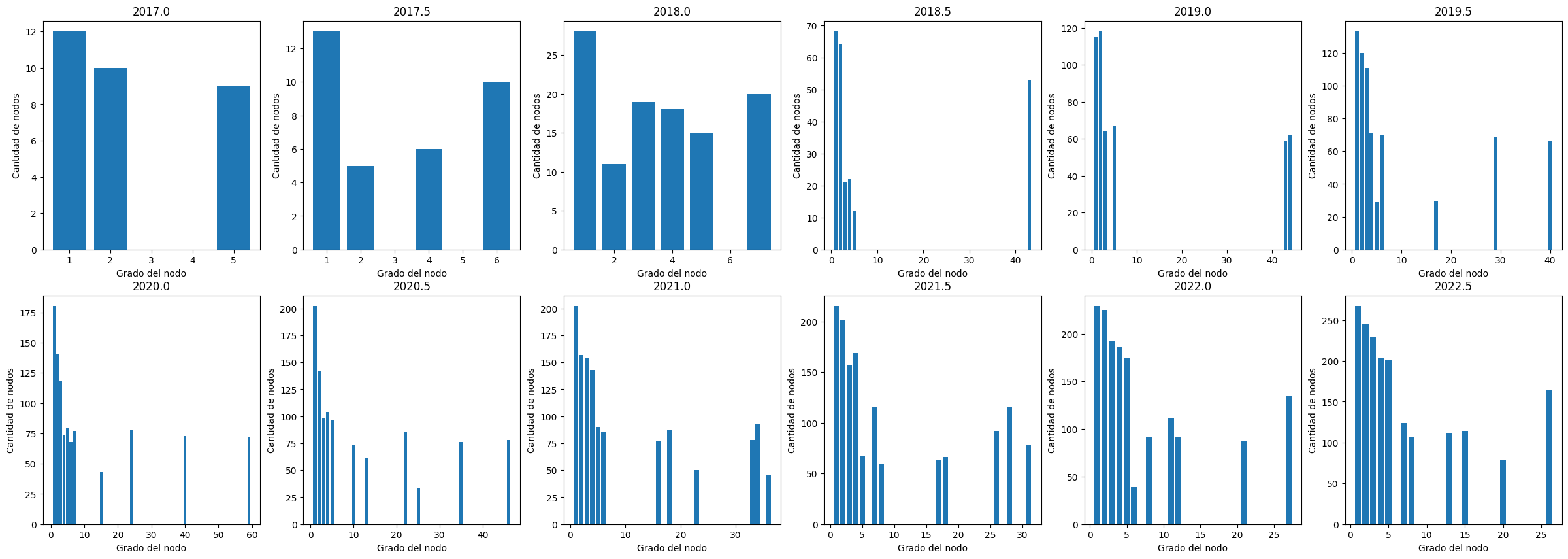
Si vemos cómo evoluciona la cantidad de nodos en relación al grado de los mismos, a partir de 2018.5, observamos que, si bien no se comporta exactamente como el modelo de Preferential Attachment, la mayoría de los nodos tienen un grado bajo hasta producirse saltos hacia grados mayores. A su vez, estos pocos con grado elevado siguen incrementándolo a lo largo del tiempo.
Habiendo dicho esto, y en conjunto con la alta densificación, se explica por qué el diámetro en la evolución se mantiene constante a lo largo de la evolución en vez de seguir creciendo, como tal vez se esperaría.
